Spider Webs
Spider webs are a structural environment in which pupils work with numbers in an abstract form and discover rules and regularities by solving a carefully thought-out series of problems.
From simple regularities and rules to equations and sequences.
Spider webs are a structural environment in which pupils work with numbers in an abstract form and discover rules and regularities by solving a carefully thought-out series of problems. They gain experience related to equations and start to understand more difficult arithmetic concepts such as arithmetic sequence or progression.
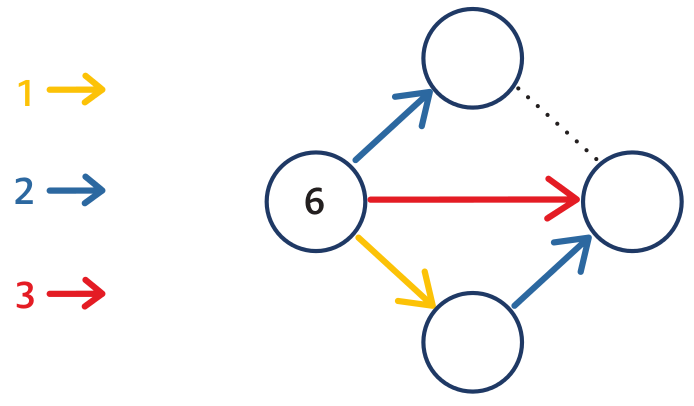
We can see four circles. In one circle, there is number 6. Our task is to fill numbers into the remaining three circles. There is also 1 yellow, 2 blue and 1 red arrows and 1 dotted line segment. The yellow arrow means “add 1”, Thus we write 7 into the bottom circle (6 + 1). The blue arrow means “add 2”. So we write 8 into the top circle (6 + 2) and 9 into the right circle (7 + 2). The red arrow adds 3. We only check that 6 + 3 = 9. The dotted line segment connects numbers 8 and 9. So we draw a yellow arrow connecting 8 to 9.
1st and 2nd grades
Problem 1: Add numbers and arrows to the spider webs.
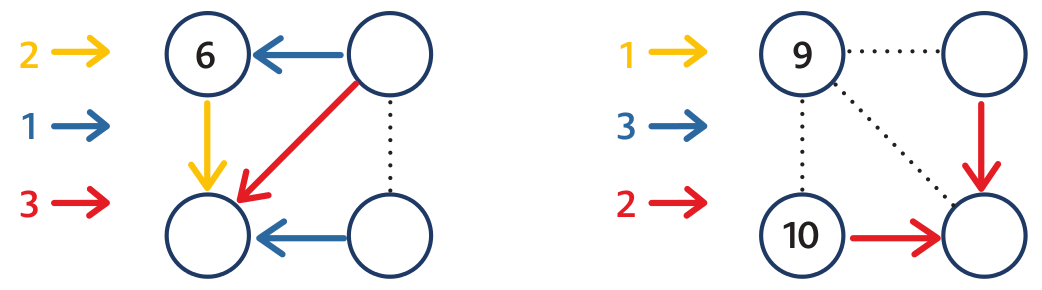
The first spider web: A blue arrow, which adds 1, leads from the right circle to number 6. Thus we look for a number which if we add 1 to it is 6. We fill in 5. Some pupil subtracts (5 = 6 – 1). We should let each pupil use their own procedure. The bottom left circle must be 8 (because 6 + 2 or 5 + 3). The bottom right circle must be 7 (because 7 + 1 = 8, or 7 = 8 – 1). We draw a yellow arrow from 5 to 7.
Having solved the second spider web some pupils notice that the two red arrows that go to the bottom right number 12 both start at the same number 10. This is the first experience that if arrows of the same colour go to the same circle, the numbers in both circles at the start of the arrow must be the same. If we want pupils to discover that it is a rule which can be used for the solution of other problems, we prepare a series of more spider webs – the first and the third spider webs in problem 2.
Problem 2: Add numbers to the spider webs and to the arrows.
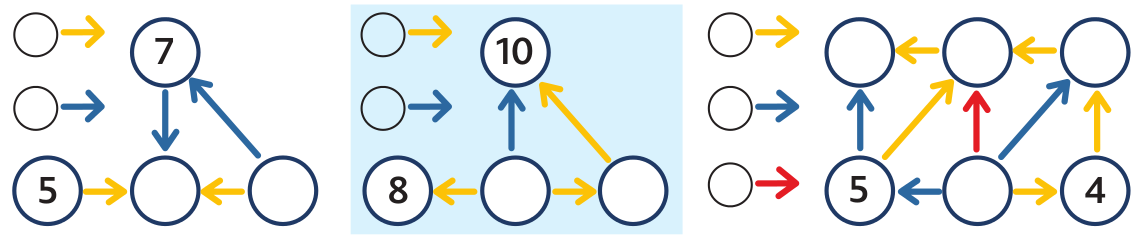The first spider web: The pupil solves it using the trial and error method. They may start e.g. by putting 6 in the middle circle. Soon they find out the spider web does not work. The blue arrows do not add the same number. So they choose another number, for example 8. The spider web does not work again. If they put 9 in the middle circle, they will solve the spider web. The number of the right is 5 and it works.
If the pupil does not notice the rule even after having solved several more problems presented, it does not matter. The pupil has worked hard, calculated a lot and got a deeper insight into the situation. They might discover the rule later or a classmate will tell them. But do not be the person who tells the pupil. Once we notice the pupil uses the rule in their solutions, we ask what would happen if we replaced 5 by 3 or 1 in the spider web. If the pupil answers that the numbers will always be the same, they have made a real discovery of the above described rule.
(In the language of mathematics, it can be expressed as: If it holds for real numbers x, y, a that x + a = y + a, then x = y).
Let us now show how pupils gain experience with solving simple equations and with arithmetic sequences.
Problem 3: Fill in.
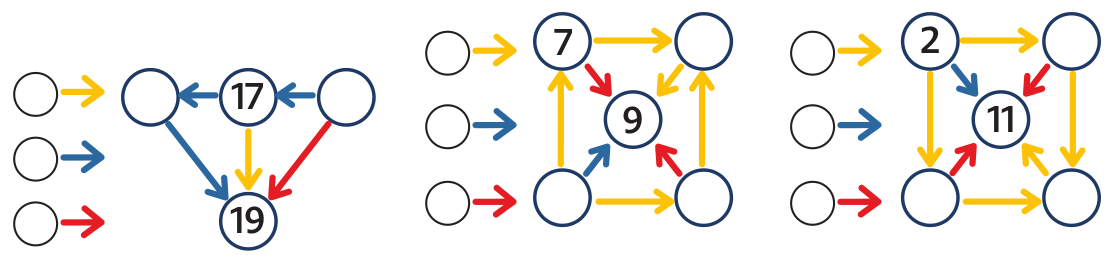
In the first spider web, we see a series of three blue arrows. The pupil sees that they will get from number 17 to number 19 using two blue arrows. The situation is so clear that we can see immediately that there is number 18 on the left. This means the blue arrow adds 1 and there is 16 in the right circle. (Recorded in the language of mathematics: 17 + 2m = 19, i.e. m = 1. Number m is the number that the blue arrow adds. We can also say that numbers 16, 17, 18 and 19 are four consecutive members of an arithmetic sequence growing by 1.)
The situation in the second spider web is similar but less clear.
In the third spider web, the three yellow arrows connect 4 numbers of an arithmetic sequence: 2, ?, ?, 11. The pupil sees: “I get from 2 to 11 using three yellow arrows. They add the total of 9, thus one yellow arrow must add 3.” The advantage of spider webs is that pupils can check easily whether the spider web works and can find a possible mistake.
3rd and 4th grades
Problem 4: Fill in the spider webs if you know that a) the least number is 5; b) the greatest number is 100; c) the sum of the least and the greatest number is 11; d) the sum of all five numbers is 15.
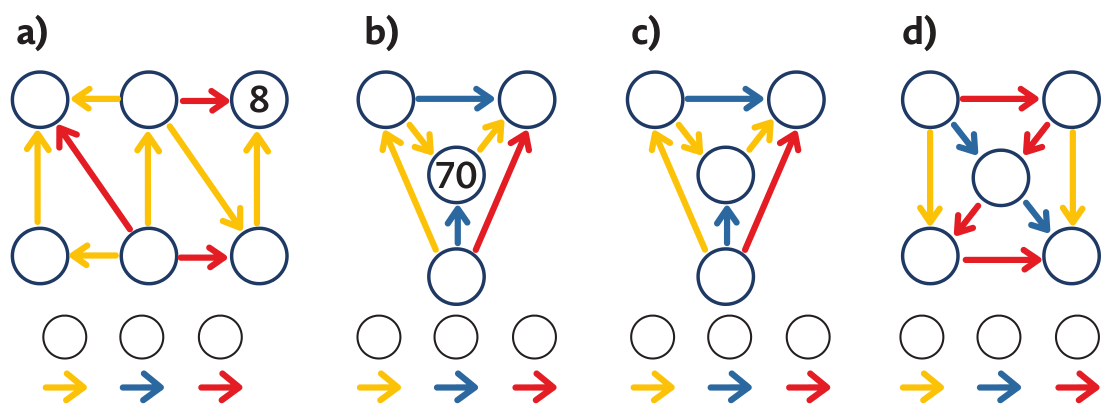
In problem a) pupils think about the position of the least number of the spider web and justify why the least number is the one where all arrows start. It is similar for the greatest number in b).
Problems c) and d) are more difficult and need many calculations. A mathematician would use the relations of the numbers in the arithmetic sequence and would solve the problem using an equation of two unknowns. In c) it is 2x + 3y = 11, in d) 5x + 10y = 15, where x is the bottom right number in the spider web and y is added by the yellow, or red arrows. The equation in c) has 2 solutions in the domain of natural numbers, the equation in d) one.
5th and 6th grades
Problem 5 opens the door to equations.
Problem 5: Select such pink number that the sum
a) of the three bottom numbers is 30;
b) of the three top numbers is 30;
c) of all six numbers is 51.
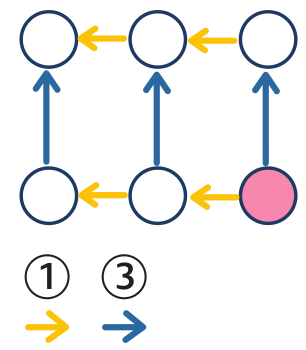
Pupils who can already work with an unknown number with the help of x, put x into the pink circle and then write x + 1 and x + 2, and to the top circles x + 3, x + 4 and x + 5.
Of course, we do not force the pupils to use a letter. They will start using them as soon as they realize they make life easier.
Comments